Blei et. al. illustrate the coordinate ascent variational inference (CAVI) using a simple Gaussian Mixture model. The model1
μ k ∼ N ( 0 , σ 2 ) z n ∼ Categorical ( 1 / K , … , 1 / K ) x n ∣ z n , μ ∼ N ( z n ⊤ μ , 1 ) \begin{aligned}
\mu_{k} & \sim \mathcal{N}\left(0, \sigma^{2}\right) \\
\mathbf{z}_{n} & \sim \text { Categorical }(1 / K, \dots, 1 / K) \\
x_{n} \mid \mathbf{z}_{n}, \boldsymbol{\mu} & \sim \mathcal{N}\left(\mathbf{z}_{n}^{\top}\boldsymbol{\mu}, 1\right)
\end{aligned} μ k z n x n ∣ z n , μ ∼ N ( 0 , σ 2 ) ∼ Categorical ( 1/ K , … , 1/ K ) ∼ N ( z n ⊤ μ , 1 ) In the following, we will derive the joint probability and CAVI update equations for the model. Finally, we use these equations to implement the model in Python.
Constructing the log joint
We start by defining the components of the model. Note that we can write the probability of the prior component means as
p ( μ ) = ∏ k N ( μ k ∣ 0 , σ 2 ) . p(\boldsymbol{\mu})=\prod_k \mathcal{N}(\mu_k|0, \sigma^2). p ( μ ) = k ∏ N ( μ k ∣0 , σ 2 ) . Similarly, the prior for the latent variables z n \mathbf{z}_n z n
p ( z n ) = ∏ k ( 1 K ) z n k p(\mathbf{z}_{n})=\prod_k \left(\frac{1}{K}\right)^{z_{nk}} p ( z n ) = k ∏ ( K 1 ) z nk while the likelihood is given by
p ( x n ∣ μ , z n ) = ∏ k N ( 0 ∣ μ k , 1 ) z n k . p(x_n|\boldsymbol{\mu}, \mathbf{z}_{n})=\prod_k \mathcal{N}(0|\mu_k, 1)^{z_{nk}}. p ( x n ∣ μ , z n ) = k ∏ N ( 0∣ μ k , 1 ) z nk . We now introduce the variables X = { x n } n = 1 N \mathbf{X} = \{x_n\}_{n=1}^{N} X = { x n } n = 1 N Z = { z n } n = 1 N \mathbf{Z}=\{ \mathbf{z}_n\}_{n=1}^{N} Z = { z n } n = 1 N p ( Z ) p(\mathbf{Z}) p ( Z ) p ( X ∥ μ , Z ) p(\mathbf{X}\|\boldsymbol{\mu}, \mathbf{Z}) p ( X ∥ μ , Z )
p ( Z ) = ∏ n ∏ k ( 1 K ) z n k and p ( X ∣ μ , Z ) = ∏ n ∏ k N ( 0 ∣ μ k , 1 ) z n k . p(\mathbf{Z})=\prod_n\prod_k \left(\frac{1}{K}\right)^{z_{nk}}\quad\text{and}\quad p(\mathbf{X}|\boldsymbol{\mu}, \mathbf{Z})=\prod_n \prod_k \mathcal{N}(0|\mu_k, 1)^{z_{nk}}. p ( Z ) = n ∏ k ∏ ( K 1 ) z nk and p ( X ∣ μ , Z ) = n ∏ k ∏ N ( 0∣ μ k , 1 ) z nk . With these equations we can construct the joint distribution which factorizes as follows
p ( X , μ , Z ) = p ( μ ) p ( X ∣ μ , Z ) p ( Z ) = ∏ k N ( μ k ∣ 0 , σ 2 ) ∏ n ∏ k ( 1 K ⋅ N ( 0 ∣ μ k , 1 ) ) z n k . p(\mathbf{X}, \boldsymbol{\mu}, \mathbf{Z})= p(\boldsymbol{\mu}) p(\mathbf{X}|\boldsymbol{\mu}, \mathbf{Z}) p(\mathbf{Z})= \prod_k \mathcal{N}(\mu_k|0, \sigma^2) \prod_n\prod_k \left(\frac{1}{K}\cdot \mathcal{N}(0|\mu_k, 1)\right)^{z_{nk}}. p ( X , μ , Z ) = p ( μ ) p ( X ∣ μ , Z ) p ( Z ) = k ∏ N ( μ k ∣0 , σ 2 ) n ∏ k ∏ ( K 1 ⋅ N ( 0∣ μ k , 1 ) ) z nk . Finally, we end up with the following log joint distribution for the model
log p ( X , μ , Z ) = ∑ k log N ( μ k ∣ 0 , σ 2 ) + ∑ n ∑ k z n k ( log 1 K + log N ( 0 ∣ μ k , 1 ) ) . (1) \log{p(\mathbf{X}, \boldsymbol{\mu}, \mathbf{Z})} = \sum_k \log{\mathcal{N}(\mu_k|0, \sigma^2)} +\sum_n\sum_k z_{nk} \left(\log{\frac{1}{K}}+ \log{\mathcal{N}(0|\mu_k, 1)}\right).\tag{1} log p ( X , μ , Z ) = k ∑ log N ( μ k ∣0 , σ 2 ) + n ∑ k ∑ z nk ( log K 1 + log N ( 0∣ μ k , 1 ) ) . ( 1 ) The variational density for the mixture assignments
To obtain the (log) variational distribution of z n \mathbf{z}_n z n ( 1 ) (1) ( 1 ) q ( μ k ) q(\mu_k) q ( μ k )
log q ∗ ( z n ) = E q ( μ k ) [ log p ( x n , μ , z n ) ] + const. = E q ( μ k ) [ log p ( x n ∣ μ , z n ) + log p ( z n ) ] + const. = E q ( μ k ) [ ∑ k z n k ( log 1 K + log N ( 0 ∣ μ k , 1 ) ) ] + const. = E q ( μ k ) [ − ∑ k z n k log 1 K + ∑ k z n k ( − 1 2 log 2 π − 1 2 ( x n − μ k ) 2 ) ] + const. = E q ( μ k ) [ − ∑ k z n k 2 log 2 π − ∑ k z n k 2 ( x n 2 − 2 x n μ k + μ k 2 ) ] + const. = E q ( μ k ) [ − ∑ k z n k 2 x n 2 − z n k x n μ k + z n k 2 μ k 2 ] + const. = ∑ k z n k x n E q ( μ k ) [ μ k ] − z n k 2 E q ( μ k ) [ μ k 2 ] + const. = ∑ k z n k ( x n E q ( μ k ) [ μ k ] − 1 2 E q ( μ k ) [ μ k 2 ] ) + const. = ∑ k z n k log ρ n k + const. (2) \begin{aligned}
\log q^{*}\left(\mathbf{z}_{n}\right) &=\mathbb{E}_{q(\mu_k)}[\log p(x_n, \boldsymbol{\mu}, \mathbf{z}_n)] +\text { const. } \\
&=\mathbb{E}_{q(\mu_k)}\left[\log p\left(x_{n} | \boldsymbol{\mu}, \mathbf{z}_{n}\right)+\log p\left(\mathbf{z}_{n}\right)\right]+\text { const. } \\
&=\mathbb{E}_{q(\mu_k)}\left[\sum_{k} z_{nk}\left(\log \frac{1}{K}+\log \mathcal{N}\left(0 \mid \mu_{k}, 1\right)\right)\right]+\operatorname{const.} \\
&=\mathbb{E}_{q(\mu_k)}\left[-\cancel{\sum_{k} z_{n k} \log \frac{1}{K}}+\sum_{k} z_{n k}\left(-\frac{1}{2} \log 2 \pi-\frac{1}{2}\left(x_{n}-\mu_{k}\right)^{2}\right)\right] +\operatorname{const.} \\
&=\mathbb{E}_{q(\mu_k)}\left[-\cancel{\sum_{k} \frac{z_{n k}}{2} \log 2 \pi} -\sum_{k} \frac{z_{n k}}{2}\left(x_{n}^2-2x_n\mu_k+\mu_{k}^2\right)\right] +\operatorname{const.} \\
&=\mathbb{E}_{q(\mu_k)}\left[-\sum_{k} \cancel{\frac{z_{n k}}{2} x_{n}^2} - z_{n k} x_n\mu_k+ \frac{z_{n k}}{2} \mu_{k}^2\right] +\operatorname{const.} \\
&=\sum_{k} z_{n k} x_n\mathbb{E}_{q(\mu_k)}[\mu_k] - \frac{z_{n k}}{2} \mathbb{E}_{q(\mu_k)}[\mu_{k}^2] +\operatorname{const.} \\
&=\sum_{k} z_{n k} \left(x_n\mathbb{E}_{q(\mu_k)}[\mu_k] - \frac{1}{2} \mathbb{E}_{q(\mu_k)}[\mu_{k}^2]\right) +\operatorname{const.} \\
&=\sum_{k} z_{n k} \log{\rho_{nk}} +\operatorname{const.} \tag{2}
\end{aligned} log q ∗ ( z n ) = E q ( μ k ) [ log p ( x n , μ , z n )] + const. = E q ( μ k ) [ log p ( x n ∣ μ , z n ) + log p ( z n ) ] + const. = E q ( μ k ) [ k ∑ z nk ( log K 1 + log N ( 0 ∣ μ k , 1 ) ) ] + const. = E q ( μ k ) [ − k ∑ z nk log K 1 + k ∑ z nk ( − 2 1 log 2 π − 2 1 ( x n − μ k ) 2 ) ] + const. = E q ( μ k ) [ − k ∑ 2 z nk log 2 π − k ∑ 2 z nk ( x n 2 − 2 x n μ k + μ k 2 ) ] + const. = E q ( μ k ) [ − k ∑ 2 z nk x n 2 − z nk x n μ k + 2 z nk μ k 2 ] + const. = k ∑ z nk x n E q ( μ k ) [ μ k ] − 2 z nk E q ( μ k ) [ μ k 2 ] + const. = k ∑ z nk ( x n E q ( μ k ) [ μ k ] − 2 1 E q ( μ k ) [ μ k 2 ] ) + const. = k ∑ z nk log ρ nk + const. ( 2 ) Here I have canceled constant terms in z n k z_{nk} z nk q ( μ k ) q(\mu_k) q ( μ k ) ( 2 ) (2) ( 2 ) log q ∗ ( z n ) \log q^{*}(\mathbf{z}_n) log q ∗ ( z n )
q ∗ ( z n ) ∝ ∏ k ρ n k z n k , q^{*}\left(\mathbf{z}_{n}\right)\propto \prod_{k} \rho_{nk} ^ {z_{n k}}, q ∗ ( z n ) ∝ k ∏ ρ nk z nk , thus in order to normalise the distribution, we require that the variational parameter ρ n k \rho_{nk} ρ nk
r n k = ρ n k ∑ j ρ n j = e x n E q ( μ k ) [ μ k ] − 1 2 E q ( μ k ) [ μ k 2 ] ∑ j e x n E q ( μ j ) [ μ j ] − 1 2 E q ( μ j ) [ μ j 2 ] r_{nk} = \frac{\rho_{nk}}{\sum_j \rho_{nj}} = \frac{e^{x_n\mathbb{E}_{q(\mu_k)}[\mu_k] - \frac{1}{2} \mathbb{E}_{q(\mu_k)}[\mu_{k}^2]}}{\sum_j e^{x_n\mathbb{E}_{q(\mu_j)}[\mu_j] - \frac{1}{2} \mathbb{E}_{q(\mu_j)}[\mu_{j}^2]}} r nk = ∑ j ρ nj ρ nk = ∑ j e x n E q ( μ j ) [ μ j ] − 2 1 E q ( μ j ) [ μ j 2 ] e x n E q ( μ k ) [ μ k ] − 2 1 E q ( μ k ) [ μ k 2 ] and the our final density is given by
q ∗ ( z n ; r n ) = ∏ k r n k z n k . (3) q^{*}\left(\mathbf{z}_{n};\mathbf{r}_n\right) = \prod_{k} r_{nk} ^ {z_{n k}}.\tag{3} q ∗ ( z n ; r n ) = k ∏ r nk z nk . ( 3 ) The variational density for the means
We proceed similarly to determine the variational density of q ( μ k ) q(\mu_k) q ( μ k )
log q ∗ ( μ k ) = E q ( z n ) [ log p ( X , μ , Z ) ] + const. = E q ( z n ) [ log p ( μ ) + log p ( X ∣ μ , Z ) ] + const. = E q ( z n ) [ log N ( μ k ∣ 0 , σ 2 ) + ∑ n z n k log N ( 0 ∣ μ k , 1 ) ] + const. = E q ( z n ) [ − 1 2 log 2 π σ 2 − 1 2 σ 2 μ k 2 + ∑ n z n k ( − 1 2 log 2 π − 1 2 ( x n − μ k ) 2 ) ] + const. = E q ( z n ) [ − 1 2 σ 2 μ k 2 − ∑ n z n k 2 ( x n 2 − 2 x n μ k + μ k 2 ) ] + const. = − 1 2 σ 2 μ k 2 + E q ( z n ) [ − ∑ n z n k 2 x n 2 + μ k ∑ n z n k x n − μ k 2 ∑ n z n k 2 ] + const. = − 1 2 σ 2 μ k 2 + μ k ∑ n E q ( z n ) [ z n k ] x n − μ k 2 ∑ n E q ( z n ) [ z n k ] 2 + const. = μ k ∑ n E q ( z n ) [ z n k ] x n − μ k 2 ( ∑ n E q ( z n ) [ z n k ] 2 + 1 2 σ 2 ) + const. = [ μ k μ k 2 ] T [ E q ( z n ) [ z n k ] x n − ( 1 2 ∑ n E q ( z n ) [ z n k ] + 1 σ 2 ) ] + const. \begin{aligned}
\log q^{*}\left(\mathbf{\mu}_{k}\right) &=\mathbb{E}_{q(\mathbf{z}_n)}[\log p(\mathbf{X}, \boldsymbol{\mu}, \mathbf{Z})] +\text { const. } \\
&=\mathbb{E}_{q(\mathbf{z}_n)}\left[\log p\left(\boldsymbol{\mu}\right) + \log p\left(\mathbf{X} | \boldsymbol{\mu}, \mathbf{Z}\right)\right]+\text { const. } \\
&=\mathbb{E}_{q(\mathbf{z}_n)}\left[\log{\mathcal{N}(\mu_k|0, \sigma^2)}+\sum_{n} z_{nk} \log \mathcal{N}\left(0 \mid \mu_{k}, 1\right)\right]+\operatorname{const.} \\
&=\mathbb{E}_{q(\mathbf{z}_n)}\left[-\cancel{\frac{1}{2}\log{2\pi\sigma^2}}-\frac{1}{2\sigma^2}\mu_k^2+ \sum_{n} z_{n k}\left(\cancel{-\frac{1}{2} \log 2 \pi}-\frac{1}{2}\left(x_{n}-\mu_{k}\right)^{2}\right)\right] +\operatorname{const.} \\
&=\mathbb{E}_{q(\mathbf{z}_n)}\left[-\frac{1}{2\sigma^2}\mu_k^2 -\sum_{n} \frac{z_{n k}}{2}\left(x_{n}^2-2x_n\mu_k+\mu_{k}^2\right)\right] +\operatorname{const.} \\
&=-\frac{1}{2\sigma^2}\mu_k^2 +\mathbb{E}_{q(\mathbf{z}_n)}\left[- \cancel{\sum_{n}\frac{z_{n k}}{2} x_{n}^2} + \mu_k\sum_{n} z_{n k} x_n - \mu_{k}^2\sum_{n}\frac{z_{n k}}{2} \right] +\operatorname{const.} \\
&=-\frac{1}{2\sigma^2}\mu_k^2 + \mu_k\sum_{n} \mathbb{E}_{q(\mathbf{z}_n)}[z_{n k}] x_n - \mu_{k}^2\sum_{n}\frac{\mathbb{E}_{q(\mathbf{z}_n)}[z_{n k}]}{2} +\operatorname{const.} \\
&= \mu_k\sum_{n} \mathbb{E}_{q(\mathbf{z}_n)}[z_{n k}] x_n - \mu_{k}^2(\sum_{n}\frac{\mathbb{E}_{q(\mathbf{z}_n)}[z_{n k}]}{2}+\frac{1}{2\sigma^2}) +\operatorname{const.} \\
&=\begin{bmatrix} \mu_k \\ \mu_k^2 \end{bmatrix}^T\begin{bmatrix} \mathbb{E}_{q(\mathbf{z}_n)}[z_{n k}] x_n \\ -(\frac{1}{2}\sum_{n}\mathbb{E}_{q(\mathbf{z}_n)}[z_{n k}]+\frac{1}{\sigma^2}) \end{bmatrix} +\operatorname{const.}
\end{aligned} log q ∗ ( μ k ) = E q ( z n ) [ log p ( X , μ , Z )] + const. = E q ( z n ) [ log p ( μ ) + log p ( X ∣ μ , Z ) ] + const. = E q ( z n ) [ log N ( μ k ∣0 , σ 2 ) + n ∑ z nk log N ( 0 ∣ μ k , 1 ) ] + const. = E q ( z n ) [ − 2 1 log 2 π σ 2 − 2 σ 2 1 μ k 2 + n ∑ z nk ( − 2 1 log 2 π − 2 1 ( x n − μ k ) 2 ) ] + const. = E q ( z n ) [ − 2 σ 2 1 μ k 2 − n ∑ 2 z nk ( x n 2 − 2 x n μ k + μ k 2 ) ] + const. = − 2 σ 2 1 μ k 2 + E q ( z n ) [ − n ∑ 2 z nk x n 2 + μ k n ∑ z nk x n − μ k 2 n ∑ 2 z nk ] + const. = − 2 σ 2 1 μ k 2 + μ k n ∑ E q ( z n ) [ z nk ] x n − μ k 2 n ∑ 2 E q ( z n ) [ z nk ] + const. = μ k n ∑ E q ( z n ) [ z nk ] x n − μ k 2 ( n ∑ 2 E q ( z n ) [ z nk ] + 2 σ 2 1 ) + const. = [ μ k μ k 2 ] T [ E q ( z n ) [ z nk ] x n − ( 2 1 ∑ n E q ( z n ) [ z nk ] + σ 2 1 ) ] + const. The last line of the derivation suggests that the variational distribution for μ k \mu_k μ k η = [ E q ( z n ) [ z n k ] x n , − ( ∑ n E q ( z n ) [ z n k ] 2 + 1 2 σ 2 ) ] \boldsymbol{\eta}=[\mathbb{E}_{q(\mathbf{z}_n)}[z_{n k}] x_n, -(\sum_{n}\frac{\mathbb{E}_{q(\mathbf{z}_n)}[z_{n k}]}{2}+\frac{1}{2\sigma^2})] η = [ E q ( z n ) [ z nk ] x n , − ( ∑ n 2 E q ( z n ) [ z nk ] + 2 σ 2 1 )] t ( μ k ) = [ μ k , μ k 2 ] t(\mu_k)=[\mu_k, \mu_k^2] t ( μ k ) = [ μ k , μ k 2 ]
s k 2 = − 1 2 η 2 = 1 ∑ n E q ( z n ) [ z n k ] + 1 σ 2 and m k = η 1 ⋅ s k 2 = E q ( z n ) [ z n k ] x n ∑ n E q ( z n ) [ z n k ] + 1 σ 2 . (4) s^2_k=-\frac{1}{2\eta_2}=\frac{1}{\sum_{n}\mathbb{E}_{q(\mathbf{z}_n)}[z_{n k}]+\frac{1}{\sigma^2}}\quad\text{and}\quad m_k=\eta_1\cdot s_k^2=\frac{\mathbb{E}_{q(\mathbf{z}_n)}[z_{n k}] x_n}{\sum_{n}\mathbb{E}_{q(\mathbf{z}_n)}[z_{n k}]+\frac{1}{\sigma^2}}.\tag{4} s k 2 = − 2 η 2 1 = ∑ n E q ( z n ) [ z nk ] + σ 2 1 1 and m k = η 1 ⋅ s k 2 = ∑ n E q ( z n ) [ z nk ] + σ 2 1 E q ( z n ) [ z nk ] x n . ( 4 ) Solving expectations
Although we have derived parameters of our variational distributions, we can't work properly with the results as all of them contain unresolved expectations. However, we can leverage the form of our variational distributions, i.e. z n k z_{nk} z nk μ k \mu_k μ k z n k z_{nk} z nk ( 3 ) (3) ( 3 )
E q ( z n ) [ z n k ] = ∑ z z n q ∗ ( z n ; r n ) = ∑ z z n ∏ k r n k z n k = r n k . (5) \mathbb{E}_{q_(\mathbf{z}_n)}[z_{nk}]=\sum_{\mathbf{z}}\mathbf{z}_n q^{*}(\mathbf{z}_n; r_n)=\sum_{\mathbf{z}}\mathbf{z}_n \prod_{k} r_{nk} ^ {z_{n k}} = r_{nk}.\tag{5} E q ( z n ) [ z nk ] = z ∑ z n q ∗ ( z n ; r n ) = z ∑ z n k ∏ r nk z nk = r nk . ( 5 ) Now we can simply plug ( 5 ) (5) ( 5 ) ( 4 ) (4) ( 4 )
σ N 2 = 1 ∑ n r n k + 1 σ 2 and μ N = r n k x n ∑ n r n k + 1 σ 2 . \sigma^2_N=\frac{1}{\sum_{n}r_{nk}+\frac{1}{\sigma^2}}\quad\text{and}\quad\mu_N=\frac{r_{nk} x_n}{\sum_{n}r_{nk}+\frac{1}{\sigma^2}}. σ N 2 = ∑ n r nk + σ 2 1 1 and μ N = ∑ n r nk + σ 2 1 r nk x n . It is easy to see that E q ( μ k ) [ μ k ] = m k \mathbb{E}_{q(\mu_k)}[\mu_k]=m_k E q ( μ k ) [ μ k ] = m k μ k \mu_k μ k r n k r_{nk} r nk 2
E q ( μ k ) [ μ k 2 ] = m k 2 + s k 2 . \mathbb{E}_{q(\mu_k)}[\mu_k^2]=m_k^2+s_k^2. E q ( μ k ) [ μ k 2 ] = m k 2 + s k 2 . Implementing the model
With these equation in hand we can easily implement the model.
class GaussianMixtureCavi:
def __init__(self, X, K):
self.X = X
self.K = K
self.m = np.random.uniform(np.min(X), np.max(X), K)
self.s = np.random.normal(size=K) \*\* 2
self.σ = 1
def fit(self):
for it in range(100):
y = self.X.reshape(-1, 1) * self.m.reshape(1, -1) - (
0.5 * (self.s + self.m**2)
).reshape(1, -1)
α = np.max(y, 1).reshape(-1, 1)
self.ϕ = np.exp(y - (α + np.log(np.exp(y - α).sum(1, keepdims=True))))
denom = 1 / self.σ + self.ϕ.sum(0, keepdims=True)
self.m = (self.ϕ * self.X.reshape(-1, 1)).sum(0) / denom
self.s = 1 / denom
def approx_mixture(self, x):
return np.stack(
[
ϕ_i * stats.norm(loc=m_i, scale=1).pdf(x)
for m_i, ϕ_i in zip(self.m.squeeze(), self.ϕ.mean(0).squeeze())
]
).sum(0)
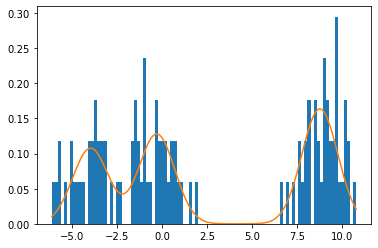
The following plot illustrates a fit of the model to simulated data with N = 100 N=100 N = 100 μ = [ − 4 , 0 , 9 ] \mu=[-4, 0, 9] μ = [ − 4 , 0 , 9 ]